談到電磁學(對,我最近開始往電磁學研究)或其他立體空間中的科學,有時不得不談談旋度。就拿我們最簡單的例子——一根無限長的載流導線而言好了。相信諸看倌都有上過國中自然課程,知道載流導線周圍會有磁場,而且在一個平面上灑上鐵粉的話,不難看出同心圓的形狀。而擺上磁針的話,可以看到許多磁針排列成以導線為圓心的圓,所以這之中一定有磁場產生磁力,讓磁針擺動。
不難發現這樣的力也是以同心圓的方式環繞在載流導線周圍,但是要如何描述力環繞導線的程度,甚至是磁場的環繞程度呢?
要更進一步了解旋度之前,我們要先引進環量(或稱漩渦量,Circulation)。很值觀地可以定義成向量對於一個封閉路徑的積分(又稱環場積分、路徑積分)。
若今有一向量場V,及一封閉路徑Γ,故得環量CircV(Γ)有:
有關路徑積分我將來還會補充。這樣的環量C畫在平面上還可以這樣表述:
「在Γ上把Γ的微小元γ和那點的向量V的點積加總起來。」
特別注意的是Γ具有方向,Γ的微小元γ也具有方向,其方向為Γ的切線方向。而點積加總起來的環量Circ則是純量。
這時就可以探討旋度了。旋度定義,即把無限小的封閉路徑Γ圍起來的面S除向量場V在該路徑Γ上的環量。當Γ無限小,S跟著無限小,Circ也應當一起無限小。大家都一起無限小,就是極限出動的時候了。
要注意的是,這個式子求出來的位於點x的旋度僅僅是σ方向的,即和面S垂直的(σ為S之法向量)。若面S是在xy平面上,那麼縮小該面求得的旋度便是z方向的。不難得出,真正的旋度應該是這樣子的:
*
或許你們會在教科書上看到一種旋度的表示方法:
而這種表示法如果讓旋度在和一個單位向量做點積的話:
雖然等號左邊是我們熟悉的旋度分量,但是等號右邊卻不是熟悉的極限,而是一個偏導數的差值。為什麼?這一塊就連維基百科也不會告訴你。
為了要證明兩種型式等價,我們先把路徑Γ弄成正方形,並且規定每個邊的長度:(其實當Γ縮到無限小時它的形狀就不重要了)
我們仍在xy平面上畫逆時鐘方向的路徑,並且在正中央定一個點叫做(x,y)。而給定向量場V的時候,路徑積分可以這麼寫:
括號上方是兩條x方向上限段各自路徑積分後加起來的值,括號下方則是y方向。
向量場V和小線段dx的點積即為向量場V在x方向的分量Vx的大小乘上小線段dx的長度。
接著把dxdy提出來,乘在一起變成小面積元dSz,這樣括號內的分母就會變成無限小了(這就是微分了!):
要注意的是第一條式子因為微分的定義本來就是y+dy要在y前面,所以要多個負號修正。
接著我們就得到向量場V在xy平面上(x,y)處的環量了。我們把他除以微小面積dSz,就剩下一個單位向量,也就是z方向的旋度。其形式和我們先前看到的旋度點積過後的幾乎一樣!!也就是說我們已經解決了xy平面方向的旋度了,接著就是yz平面方向和xz平面方向,三個方向共同組成整個向量場的旋度。
*
基本上,如果向量場很單純地只和xy座標有關(即無論z多少其向量都一樣,可以想成一個圓柱),只要求z方向的旋度即可(面構築在xy平面)。例如我們剛開始看過的向量場:
現在在xy平面上畫一條橘色的圓形路徑Γ,並給他一個逆時鐘的方向。
若以r代表向量場中任意點至原點的距離,可得到Γ圍起來的面積是πr^2,而Γ的長度是2πr。那就是,我們要路徑積分的長度將會是2πr。而又Γ上任意一點至原點等距離,那點相對應的向量場大小也會恆等(看出來了嗎,這個向量場大小只和原點距離有關),方向也和Γ相同。因此路徑積分可以簡化成Γ長度乘上Γ上向量場大小。我們得到了其數值為2πr^2。
此時再把面積除下去,並朝向原點O縮小,可以得到z方向的旋度,也是這個向量場唯一的旋度:
旋度的表示法除了CurlV以外尚有rotV和∇×V。而CurlV=2z代表的是整個向量場的旋轉程度為2,也可以解釋成對於任何點造成的旋轉程度為2。
*
有時候我們不得不使用那個看起來很麻煩的表述法,因為那樣比較好求旋度。例如這個向量場:
這時畫路徑求旋度似乎有點困難,而且同時我們想知道這個向量場整個旋度的分布狀況,因此使用了那個很麻煩的表述法:
*
旋度比散度好理解太多了。
*
有關LaTeX的語法:


.gif)

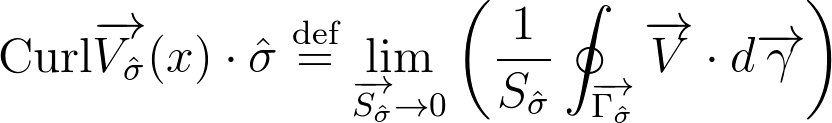.gif)
.gif)
.gif)

.gif)
.gif)
.gif)




.gif)

.gif)

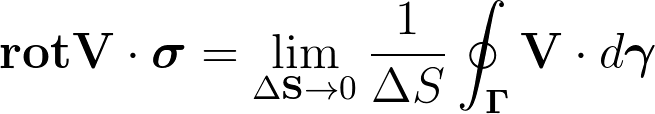
hi
回覆刪除