散度最為人知的地方在於點電荷的電場。由於單一正電荷的電力線是向外發散的,因此我們可以計算它的散度。
和旋度同一掛,散度(Divergence)也是向量分析的一員。既然證過了旋度,那麼散度也應該不會難到哪裡去了,比較大的差別就是散度會牽扯到三維空間。
就和旋度有環量在支撐一樣,在談散度前我們也要來談談通量(Flux)。就是那個電通量和磁通量,對了!
所謂通量,就是向量場對於有向曲面的積分。也就是說,通量和環量一樣,是個純量。假設有個向量場V,以及一個有向曲面Σ及微小面元σ(方向垂直表面),那麼通量ΦV(Σ)可以這麼寫:(粗體者為向量)
這裡有兩個積分符號的曲面積分,對應到環量的路徑積分,也可以理解為「把向量場V和微小面元σ的內積加總起來」。而由於微小面元σ可以是由任意兩個方向的微小元共同組成,因此也可以說是「加總兩次路徑積分」。
那麼現在就來談談散度吧。如同旋度是由環量除以無限小的面積,散度的定義是把無限小的有向曲面Σ上向量場V對微小面元σ的曲面積分除以曲面Σ所圍成的體積Δφ,而且曲面Σ的方向是由內而外的。
和旋度不同的是散度是純量。
*
可是三維的散度在計算上不像旋度那麼簡單(尤其是封閉曲面的表述方法),因此我們不得不使用那個麻煩的散度表述方法,而我將會再次證明這條公式。
首先我們來建構一個無限小正方體,各個邊的邊常都是dxdydz,在正方體中間有一個點P(x,y,z),而正方體的六個面構成有向曲面Σ。
此時再賦予一個向量場V。依照曲面積分的線性性質,對於整個表面積的積分可以看成六片面積的積分的加總,故得:
接著再各取V的分量,並把負號提出來:
接著再把dxdydz提出來:
很有偏微分的味道了對吧?
這樣我們就有了微小正方體的通量了。接著定義微小體Δφ為dxdydz:
把通量除以微小體Δφ,就是我們要的散度了。
*
有關公式的LaTeX語法:
\textup{div}\mathbf{V}=\frac{\partial V_x}{\partial x}+\frac{\partial V_y}{\partial y}+\frac{\partial V_z}{\partial z}





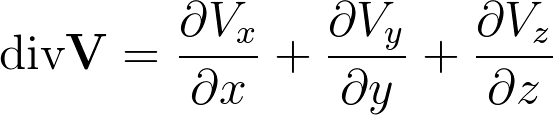







沒有留言:
張貼留言